Tot de belangrijkste leerstof van groep 4 behoren in ieder geval de tafels van vermenigvuldiging van 1 tot en met 10. Aan het eind van dit leerjaar moeten leerlingen deze vlot uit het hoofd kennen; op volgorde en door elkaar.
Hiervoor heb je als leerkracht 40 schoolweken de tijd. Iedere schoolweek heeft doorgaans 5 rekenlessen van een uur en dus heb je 200 uren beschikbaar. Natuurlijk moet je ook nog andere rekenleerstof onderwijzen, maar de hoeveelheid tijd is overweldigend.
Toch lukt het vaak niet om alle kinderen de tafels te leren. Hoe dit kan? Het ligt in ieder geval lang niet altijd aan de leerkracht. Sommige Nederlandse uitgevers van rekenboeken maken het namelijk onnodig ingewikkeld voor de mensen voor de klas en voor de leerling. Dat zal ik toelichten.
Eerst leg ik uit hoe je de tafels op een doelmatige manier aanleert. Daarna zal ik laten zien hoe deze worden onderwezen in de rekenboeken die veel scholen gebruiken. Ik zal het krachtig, kort en begrijpelijk houden.

De effectieve manier
Eerst de doelmatige aanpak. Deze kun je zelfs zonder rekenboeken toepassen. Je hebt enkel pen, papier, fiches en een schoolbord nodig. We beginnen met de tafel  van 2.
Je deelt fiches uit en laat de kinderen groepjes van 2 maken. Hierbij leg je uit dat je het eerste groepje 1 x 2 fiches is en noteert op je bord de bijpassende tafelsom met antwoord. De leerlingen schrijven dit mee in hun rekenschrift. Aan het eind van de les staat de tafel van 2 overzichtelijk op het bord en in de schriften van de kinderen.

Figuur 1   Leerlingwerk bij de tafel van 2

In de tweede les laat je de tafel op volgorde oefenen en uit het hoofd leren door de antwoorden af te dekken. De derde les gebruik je om de tafel door elkaar te oefenen. Hierna kies je een nieuwe tafel die je op dezelfde wijze aanleert. Je voegt vervolgens een les toe waarin je ook beide tafels door elkaar laat oefenen. Een werkblad met 100 sommen is eenvoudig gemaakt met sommenmaker.nl. Geen hogere wiskunde.

Figuur 2   Werkblad met de tafels van 2 en 5 door elkaar

De ingewikkelde manier
Maar zo gaat het helaas niet in veel rekenboeken. In plaats dat de tafels worden onderwezen en ingeoefend worden deze ‘verkend’ en moeten ze worden ‘begrepen’.
Dus in plaats van duidelijk uit te leggen en structuur aan te brengen, verandert de rekenles in een warrige exercitie met strategieën als 1x meer, 1x minder, verdubbelen, halveren en omkeren. Dat betekent dat kinderen slechts de tafelsommen 1×2, 5×2 en 10×2 uit hun hoofd hoeven te leren. Alle andere sommen kunnen ze uitrekenen aan de hand van deze steunsommen.

Ze rekenen 9×2 uit door als steunsom 10×2=20 te nemen en daarvan 2 af te trekken. Voor 8×2 moet nogmaals 2 worden afgetrokken. Een som als 6×2 rekenen ze uit door 2 op te tellen bij 5×2.

Kinderen leren ook verdubbelen en halveren. Als 4×2 als antwoord 8 heeft, dan is 8×2 het dubbele, dus 8+8=16. Net zoals ze 4×2 kunnen uitrekenen door de helft van 8×2 te nemen. Dat ze nog niet hebben leren delen is blijkbaar geen probleem.

Een som als 2×9 wordt ook al aangeboden, ondanks dat de tafel van 9 nog niet is onderwezen. 2×9 is immers hetzelfde als 9×2 (omkeren). En dat kunnen ze dan weer uitrekenen door 10×2 als steunsom te nemen en daarvan 2 af te trekken. Zo kun je ook gerust al 9×8 vragen, want dat is 1×8 minder dan 10×8. Dat ze de tafel van 8 nog niet kennen is geen probleem, want ze moeten immers de strategie van 1x minder leren en niet de tafels.

Het uit het hoofd leren van de tafels is vervangen door het toepassen van strategieën, want iets uit het hoofd kennen is ouderwets en mechanisch en hindert daarmee het begrip volgens de bedenkers van deze aanpak. Hoe zo’n les eruitziet, liet een leerkracht onlangs op X zien.

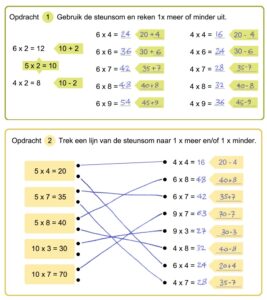
Figuur 3   Rekenopdrachten in een hedendaags rekenboek (bewerking)

Wanhopige leerkrachten
Volg jij het nog? Veel kinderen in de rekenlessen die ik observeer niet! Laatst begon een leerkracht zelfs te huilen tijdens het feedbackgesprek dat ik met haar voerde, omdat het rekenboek haar het lesgeven wel heel erg moeilijk maakte. Ik kon haar frustratie goed invoelen.
Een andere leerkracht van een groep 4 mailde mij met de vraag wat te doen met dit soort lessen en of ze nog wel tafels mag oefenen met haar leerlingen. Dit oefenen wordt door rekenexperts namelijk schamper aangeduid als ‘stampen’.

Beste Marcel,

 In groep 4 en 5 blijken de geboden strategieën die ik eerder noemde voor een groot aantal leerlingen veel tijd te kosten bij het komen tot de uitkomst. En dan heb ik het nog niet over de leerlingen die sommen over het tiental nog niet vlot uitgerekend kunnen krijgen en daardoor ontmoedigd raken of verkeerde uitkomsten geven. Onze rekencoördinator heeft juist dit jaar haar opleiding afgesloten en zegt dat het stampen niet meer mag. 

Een leerkracht van groep 4

Lage verwachtingen
Het onderwijzen van de tafels wordt onnodig ingewikkeld gemaakt en daarmee komen leerlingen in de problemen als ze in groep 5 moeten gaan delen en cijferend vermenigvuldigen.
Daar komt nog eens bij dat in sommige rekenboeken niet alle tafels meer worden onderwezen in groep 4, maar enkel de tafels van 2, 3, 4, 5 en 10. Bedenk hierbij: als iets niet wordt aangeboden, dan wordt het niet geleerd. Lage verwachtingen leiden tot slechte rekenresultaten. In 1963 moesten kinderen eind groep 4 (klas 2) nog alle tafels tot en met 20 kennen, zo valt te lezen in de ‘Leidraad Inspectie van het Lager Onderwijs’ van datzelfde jaar.

Leer ze rekenen
De tafels van vermenigvuldiging behoren tot de 20 procent belangrijkste leerstof van groep 4. Een slechte beheersing ervan bemoeilijkt de hele verdere schoolcarrière. Laten we deze daarom helder uitleggen en gestructureerd inoefenen. Als de rekenboeken het niet doen, pak dan pen, papier, fiches en je schoolbord en leer ze rekenen!

Geschreven door Marcel Schmeier
Illustraties: Marcel Schmeier (1), Sommenmaker.nl (2) en Ruud Bijman (3)

Meer weten over effectief rekenonderwijs? Lees dan het boek!